Aufbau eines Neuons

Ein Neuron bildet die Recheneinheit eines neuronalen Netzes ab und verrechnet ein oder mehrere Eingangswerte x zu einem Ausgangswert ȳ. Es besteht aus den folgenden drei Komponenten:

• Gewichtungen w werden mit Eingangswerten multipliziert und verändern diese. Da die Eingangswerte statisch sind und sich nicht anpassen können, sind Gewichtungen notwendig. Durch die Veränderungen einer Gewichtung ändern sich gleichzeitig alle Eingangswerte die mit dem Gewicht multipliziert werden. So kann sich das Netz anpassen, daher bilden die Gewichtungen den flexiblen Teile eines neuronalen Netzes ab.

• Die Aktivierungsfunktion a dient als Schwellwert. Dazu wird die Aktivierungsfunktion auf den Ausgabewert eines Neurons angewendet. Je nach Implementierung skaliert die Aktivierungsfunktion den Wertebereich der Ausgabematrix, sodass der Wert ganz, teilweise oder gar nicht an das nächste Neuron weitergeleitet wird. Die bekanntesten Aktivierungsfunktionen sind Sigmoid, Relu und SoftMax

  1. Sigmoid begrenzt den Zahlenbereich auf +1 bis 0. Daher gibt ein vollständig aktiviertes Neuron eine 1 zurück. Gleichzeitig schwächen sich Werte unterhalb der Aktivierung exponentiell ab.

  2. Relu ersetzt alle negativen Werte durch 0, alle anderen Werte bleiben erhalten. Somit zeichnet sich die Relu Berechnung durch eine höhere Geschwindigkeit aus.

  3. SoftMax gibt die Wahrscheinlichkeit aller Klassifizierung zurück. Daher wird der jeweilige Zahlenwert durch die Summe aller Zahlenwerte geteilt. Die SoftMax Funktion wird in der letzten Schicht eines neuronalen Netzes verwendet und konvertiert die Ausgabe aller Klassifizierungen in Prozentwerte zwischen 0 und 1.

• Das Bias b gibt einen zufälligen Wert zurück und wird auf die Ausgabe der anderen Neuronen addiert. Dadurch wird der Ausgabewert eines Neurons zufällig verschoben, was verhindert, dass ein neuronales Netz eine falsche Funktion lernt und erlaubt zwischen verschiedenen Funktionen zu variieren.

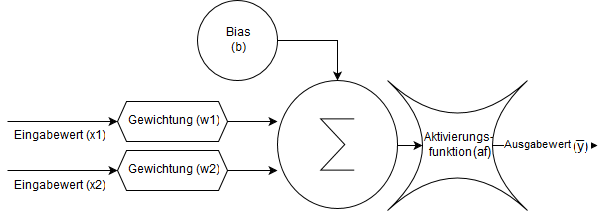
Das Schaubild zeigt die Funktionsweise eines Neurons. Die einzelnen Pfeile geben den Datenfluss an. Die Gewichtungen sind als Sechsecke eingezeichnet und werden mit den Eingabewerten multipliziert. Das Bias ist als runder Kreis dargestellt und fließt wie die Eingabewerte ebenfalls in die Summenfunktion des Neurons ein. Anschließend wird die Summe mit einer Aktivierungsfunktion zu einem Ausgabewert verrechnet. Mathematisch wird ein Neuron wie folgt beschrieben:

$ȳ = a(\sum_{i=1}^{n} (x_{i} * w_{i}) + b)$

Die Gleichung zeigt die Berechnung eines Neurons mit n gewichteten Eingangswerten. Diese werden aufsummiert und anschließend mit dem Bias verrechnet. Zuletzt wird die Aktivierungsfunktion auf die Summe angewendet um den Ausgangswert ȳ zu berechnen.

Ressourcen

http://www.u-helmich.de/bio/neu/1/11/111/seite1111.html

http://www.deeplearningbook.org

https://jeremykun.com/2012/12/09/neural-networks-and-backpropagation/