Schichten eines neuronalen Netzes

Ein neuronales Netz besteht wie in Aufbau eines Netzes vorgestellt aus verschiedenen Schichten. Jede Schicht implementiert andere mathematische Funktionen in den zugehörigen Neuronen. So löst jede Schicht eine andere Problemstellung.

Fully Connected Layer

In einem Fully Connected Layer (oft auch als Dense Layer bezeichnet) ist jedes Neuron des vorherigen Layers mit jedem Neuron des aktuellen Layers verbunden. Durch seinen Aufbau fließen die Berechnungen jedes vorherigen Neurons in die Berechnung des aktuellen Neuronen ein. So entstehen viele Abhängigkeiten die nicht alle relevant sind aber viel Rechenleistung benötigen. Andererseits bringt das Fully Connected Layer den Vorteil, das alle Neuronen gleich bewertet werden. Durch diese Generalisierung ist des Fully Connected Layer auf allen eindimensionalen Daten anwendbar und trifft keine Entscheidungen über die Art der Daten. Wegen dieser Eigenschaften kommt ein Fully Connected Layer oft am Ende eines Netzes zum Einsatz, wo Beziehungen zwischen wenigen hoch aggregierten Daten abgebildet werden.

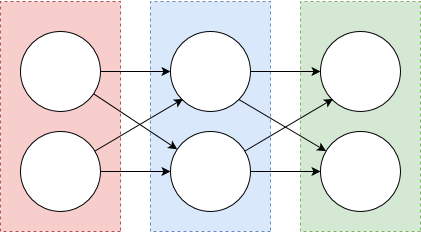
Ein Beispiel für ein Fully Connected Layer wird im Abbild aufgezeigt, indem alle Neuronen über Pfeile miteinander verbunden sind.

Convolutional Layer

Das Convolutional Layer ist auf die Verarbeitung von mehrdimensionalen Bilddaten ausgelegt. Es erfasst Nachbarkorrelationen zwischen Daten indem die umliegenden Datenpunkte bei der Berechnung mit einfließen. Dazu wird ein gewichteter Kernel (oft auch Filter genannt) über die Daten bewegt. Da nicht alle Abhängigkeiten miteinbezogen werden, sondern nur die benachbarter Pixel, wird weniger Rechenleistung benötigt. Daher werden irrelevante Beziehungen zwischen Datenpunkten ausgeschlossen. Zusätzlich erlernt das Convolutional Layer über die verschiedenen Kernel unterschiedliche Arten von Pixelregionen, die sich im Bild wiederholen. So werden in einem Netz aus mehreren Convolutional Layern anfänglich Ecken und Kanten über einen Kernel erkannt und in den folgenden Layern immer weiter aggregiert.
Dazu bildet jeder Kernel eine eigene Ergebnismatrix ab. Diese wird aus den Ergebnissen der Multiplikation des zugehörigen Kernel auf einen Datenausschnitt um einen relevanten Datenpunkt und der anschließend Summierung der Werte gebildet. Befindet sich der jeweilige Datenpunkt am Rand und hat somit keinen vollständigen Datenausschnitt, wird er je nach Implementierung weggelassen oder über verschiedene Padding Strategien miteinbezogen.

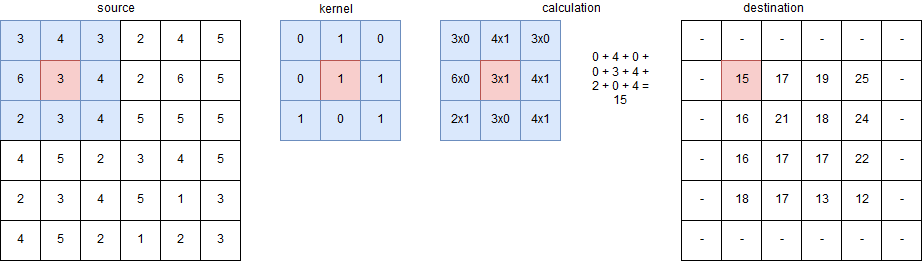
Das Abbild zeigt die Schritte eines Convolutional Layer. Dazu ist ein 3 x 3 großer Kernel (Convolutional Kernel) dargestellt. Der Kernel enthält verschiedene null und eins Gewichtungen. Die einzelnen Gewichtungen werden mit einem Datenausschnitt (blau markiert) um den jeweils mittigen Datenpunkt (rot markiert) multipliziert und aufsummiert. Der Ablauf der Berechnung ist im Schaubild dargestellt. Die Summe minus 15 wird in der Ergebnismatrix des Kernels abgebildet. Der Kernel bewegt sich über die gesamte source Matrix und berechnet die destination Matrix. Ist es nicht möglich eine 3 x 3 Matrix um einen Datenpunkt zu legen wird der Datenpunkt nicht berechnet (-). Diese Paddingstrategie wird als "Valid" bezeichnet.

Pooling Layer

Das Pooling Layer verarbeitet ebenfalls mehrdimensionale Daten, indem es eine vorgegebene Matrix aus Datenpunkten (Kernel) zusammenfasst und auf eine Ergebnismatrix abbildet. Dabei werden alle Werte des Kernels durch einen Wert ersetzt. Die Anzahl der Datenpunkte reduziert sich so um die Kernelgröße. Je nach Implementierung wird der Maximalwert oder der Durchschnittswert des Kernels in der Ergebnismatrix abgebildet.
Durch das Pooling Layer wird die Datengröße reduziert, was die Berechnung der folgenden Layer beschleunigt. Zusätzlich reduziert das Pooling Layer die Einwirkung von Translation und Rotation durch die Reduktion von Abhängigkeiten und ermöglicht eine bessere Abdeckung der folgenden Layer durch die Aggregation einzelner Datenpunkte.

Max Pooling Layer ist das meist genutzte Verfahren. Hier wird der Maximalwert des Kernels in die Ergebnismatrix geschrieben.
Average Pooling Layer nimmt den Durchschnitt der Werte in einem Kernel. Der Durchschnittswert wird in der Ergebnismatrix eingefügt.

Das Schaubild skizziert den Ablauf des Max Pooling Layers mit einem 2 x 2 Kernel. Dabei wird der Maximalwert aus der jeweiligen roten, grünen, gelben und blauen Matrix in die Ergebnismatrix abgebildet. Die anderen Werte der Matrizen werden nicht in die Ergebnismatrix aufgenommen.

Transpositional Convolutional Layer

Das Transpositional Convolutional Layer (Deconvolutional Layer) überschneidet sich mit dem im Abschnitt vorgestellten Convolutional Layer indem es ebenfalls durch Kernel mehrere Ergebnismatrizen abbildet. Allerdings erweitert es die Funktionalität indem es gleiche Datenpunkte der Ergebnismatrizen zusammenführt um die Features der Eingangsdaten zu rekonstruieren. Die einzelnen Kernel bilden dabei die semantische Informationen auf den Datenpunkten ab. So wird jeder Pixel einem möglichen Label zugewiesen. Die Aggregation der Information auf einen Pixel ermöglicht eine Skalierung der Bilddaten bei gleichzeitigem Verstärken der semantischen Informationen und Unterdrücken von Bildrauschen.

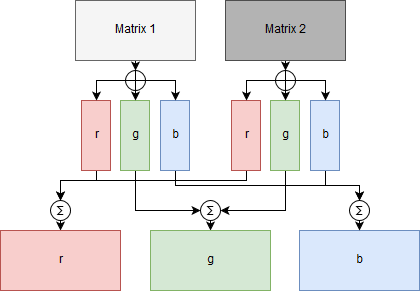
Die Darstellung zeigt die Funktion des Transpositional Convolutional Layer. Dazu werden drei Kernel (rot, grün, blau) festgelegt, die auf alle zwei Eingangsmatrizen angewendet werden. Die Funktionsweise der Kernel ist die gleiche wie bei einem Convolutional Layer. Durch die Anwendung der drei Kernel auf die zwei Eingangsmatrizen entstehen sechs Teilergebnismatrizen. Jeweils drei für jeden Eingangsvektor. Anschließend werden alle Teilergebnismatrizen, die mit dem gleichen Kernel erzeugt wurden zusammengefasst. So entstehen drei Ergebnismatrizen die jeweils alle roten, grünen oder blauen Teilergebnismatrizen enthalten.

Unpooling Layer

Das Unpooling Layer ist das Pendant zum Pooling Layer. Dazu wird die Eingangsmatrix um die Kernelgröße skaliert. Da die Reduktion der Daten im Pooling Layer verlustbehaftet ist, nutzt das Unpooling Layer Metadaten, sogenannte Switches aus dem Pooling Prozess, um die ursprüngliche Position der Maximalwerte zu ermitteln. So ist nicht nur die Reduzierung der Datenpunkte umkehrbar, sonder auch der Verlust an Datenpunkten lässt sich ausgleichen. Durch das Wiederherstellen der Datenpunkte an der vorherigen Position, ist trotz des Verlustes an Datenpunkten eine gute Auflösung der Skalierung möglich.

Das Schaubild zeigt in drei Schritten die Datenreduktion durch das Pooling Layer sowie die Skalierung durch das Unpooling Layer. Im Pooling Layer (links) wird die 4 x 4 Eingangsmatrix mit einem 2 x 2 Kernel auf die Größe 2 x 2 reduziert. Dabei entsteht die Ausgangsmatrix (Pooled Map) mit den Maximalwerten des jeweiligen Kernels (grün, gelb, rot, blau) sowie eine Matrix, die die vorherige Position des Maximalwertes (Switches) beinhaltet. Im Unpooling Layer (rechts) werden die 2 x 2 Eingangsmatrizen mit einem 2 x 2 Kernel in eine 4 x 4 Ausgangsmatrix überführt. Dazu wird die Position der Maximalwerte mithilfe der Switches errechnet. Die anderen ursprünglichen Werte lassen sich nicht wiederherstellen, daher werden sie mit einer Null gefüllt.

Dropout Layer

Ein Dropout Layer deaktiviert eine vorgegebene Anzahl an Neuronen. Die deaktivierten Neuronen werden nach einem zufälligen Schema getauscht und fließen nicht in die folgenden Berechnungen anderer Layer ein. Um ein effizientes Lernen zu gewährleisten, werden die deaktivierten Neuronen nach jedem Datensatz gewechselt.

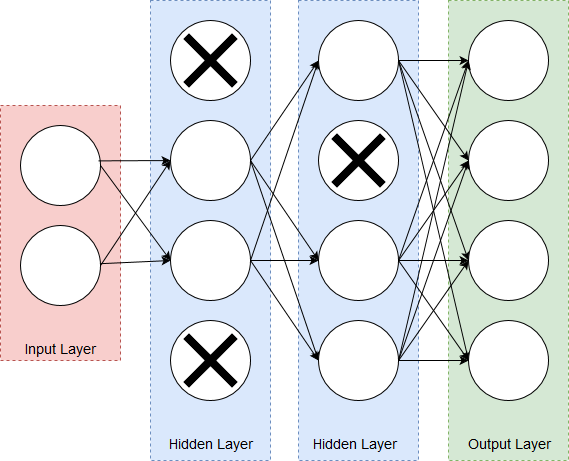
Durch die reduzierte Anzahl an Neuronen wird Overfitting verhindert, indem ein Netz die gleichen Ergebnisse über unterschiedliche Neuronen errechnet. Gleichzeitig erhöht das Dropout Layer die Robustheit des Netzes, da zufälliges Rauschen eingeführt wird und beschleunigt das Netz da einige Neuronen nicht mehr berechnet werden. Ein Dropout Layer ist nur während der Trainingsphase aktiv, da das zufällige Deaktivieren von Neuronen beim Errechnen eines optimalen Labels zu unterschiedlichen und auch falschen Ergebnissen führen würde. Das Abbild zeigt ein neuronales Netz mit aktiven Neuronen links und deaktivierten Neuronen rechts.

Batch Normalization Layer

Ändert sich die Ausgabe eines Layers, müssen die nachstehenden Layer eine neue Ausgabe sowie eine neue Verteilung der Ausgabewerte erlernen. Dieses Verhalten wird als Internal Covariate Shift bezeichnet. Um diesem Effekt entgegenzuwirken wird das Batch Normalization Layer verwendet. So reduziert sich die Trainingszeit da die Anpassung einzelner Layer entfällt. Gleichzeitig erhöht das Batch Normalization Layer die Robustheit des Netzes, da zufällige Neuronen normalisiert werden, wird ein Rauschen eingeführt.
Das Batch Normalization Layer normalisiert die Ausgabe der Aktivierungsfunktionen über einen Mini-batch. Ein Mini-batch entspricht dabei einer geringen Anzahl von Datensätzen.
Zur Berechnung wird der Durchschnitt des Mini-batch von jedem Ausgabewert der Aktivierungsfunktionen abgezogen. Anschließend wird das Ergebnis durch die Standardabweichung des Mini-batch geteilt. Zum Schluss werden die Werte mit einem Faktor $\gamma$ skalliert und einem Parameter $\beta$ addiert. Durch die Normalisierung der Eingaben werden Funktionen besser generalisiert. So ist ein abstrahiertes Lernen von Funktionen auf nicht optimalen Daten möglich.